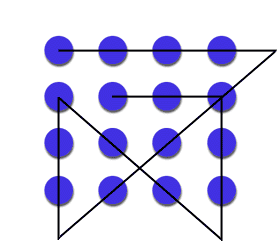
PROBLEM: 
An Arab sheikh tells his two sons to race their camels to a distant city to see who will inherit his fortune.  The one whose camel is slower will win.  The brothers, after wandering aimlessly for days, meet a wise woman and ask for advice. After talking to her they immediately jump on the camels and race as fast as they can to the city.  What did the wise woman tell them?

PROBLEM:
Given twelve coins that are identical in size, shape, and color, determine which single coin is heavier or lighter in weight than the others.  You are supplied with a balance and must conclude your determination in three weighings.

PLEASE NOTE: This problem is very difficult, because your answer must solve for both possible outcomes (heavier and lighter) all within 3 weighing.

PROBLEM:
Rearrange three golfballs so that the triangular pattern points down instead of up.

.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:

PROBLEM:
Four rollerbladers exercise around separate circular paths; each path is one third of a mile in length.  They start simultaneously at the black spots, with speeds of six, nine, twelve, and fifteen miles per hour.  By the end of the 20 minute workout, how many times will they have simultaneously returned to the spots where they started?In 1/3 of an hour (20 minutes), they travel 1/3 of a mile 6, 9, 12, and 15 times.  The largest number these numbers are all divisible by is 3.  They return to their original positions 3 times in 20 minutes: after 6 2/3, 13 1/3, and 20 minutes

PROBLEM:
Gears A and D have 60 teeth each, gear B has 40 teeth, and gear C has 20 teeth.  Suppose that gear B makes twenty complete turns every minute, explain the relative speed of gears A and D?
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:
Gears A and D rotate at the same speed.  Gears of equal size will rotate at constant speeds irrespective of smaller or larger gears in between them

PROBLEM:
How many triangles are located in the image below?
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:
27 triangles.  There are 16 one-cell triangles, 7 four-cell triangles, 3 nine-cell triangles, and 1 sixteen-cell triangle.

PROBLEM:
How many squares can you create in this figure by connecting any 4 dots (the corners of a square must lie upon a grid dot)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

SOLUTION:

PROBLEM:

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:
The image on the left illustrates where the cut is made, and the image on the right rearranges the cutout piece clockwise (180 degrees) to place the hole in the center of the square! 

PROBLEM:
Place the numbers 1 through 9 in the circles below, such that each side of the triangle adds up to 17.
 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:

PROBLEM:
How is it possible to trace this design in one continuous movement without crossing a line on the way?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


SOLUTION:

PROBLEM:
Remove six matches to make ten.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:

PROBLEM:
Complete the square logically.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


SOLUTION:

Each symbol is associated with another's position; this upside-down spade is always to the left of a right-side-up heart

PROBLEM:
If teapot A holds 32 ounces of tea, about how many ounces does teapot B hold?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:
16 ounces (about half of pot A).  The amount of tea that can be kept within each pot is determined by the height of the spout opening.  The tea level cannot rise above the spout opening since any extra tea would merely spill out from the spout.  A simple visual estimate would conclude that the spout of teapot B is approximately half the height of that of teapot A, therefore providing only half of the capacity, or 16 ounces

PROBLEM:
Using six contiguous straight lines, connect all of the sixteen circles shown below.
























.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:

  

PROBLEMIn three moves, rearrange the coins so that the three quarters are together and the two pennies are together with no empty space in between each coin.  At the end of each move, the coins are always in a line as in the original configuration.  Each move consists of moving two adjacent coins at one time
    
.
.
.
.
.
.
.
.
.


.
.
.
.


.
.
.
.
.
.


.
.
.
.
.
.





SOLUTION (original)

PROBLEM:
If you look, you can't see me.
If you see me, you cannot see anything else.
I can make you walk if you can't.
Sometimes I speak the truth.
And sometimes I lie.

What am I?.
.
.
.
HINT 1:
Question: Is "I" something tangible, that can be felt or touched?

Answer: No.
.
.
.
HINT 2:
Question: Is it something that happens at specific times?

Answer: Yes.
.
.
.
.
SOLUTION:
A dream

PROBLEM:
A man was walking along a railway track when he spotted an express train speeding towards him.  To avoid it, he jumped off the track, but before he jumped he ran ten feet towards the train.

Why?.
.
.
.
.
HINT 1:
Question: Could the man have run less than 10 feet and still avoided the train?

Answer: No.
.
.
.
HINT 2:
Question: Was the train steam-powered?

Answer: Yes



Question: Did the train's whistle blow just before the man started to run?

Answer: Yes 
. .
.
.
.
.
.
.
SOLUTION:
The man was walking through a train tunnel and was almost at the end when he heard a whistle and spotted the train coming towards him.  He therefore had to move forward, towards the train, so that he could jump clear safely.

PROBLEM:
A man and his son were traveling on a scheduled flight across the Atlantic.  The man asked the flight attendant if his son could have a look inside the cockpit.  The boy was allowed to do this and the pilot gladly explained about the plane and its controls.  After the boy left, the pilot turned to the co-pilot and said to him, "That was my son."

How could that be?.
.
.
.
.
.
HINT 1:
Question: Were any stepfathers, grandparents, or in-law relationships involved?

Answer: No.
.
.
.
HINT 2:
Question: Was the passenger the father of the pilot's son?

Answer: Yes.
.
.
.
.
.
SOLUTION:
The pilot was the boy's mother.

PROBLEM:
A man is dead in a puddle of blood and water on the floor of a locked windowless room.  What happened?.
.
.
.
HINT 1:
Question: Was any other person, object, weapon, or other item in the room?

Answer: No.
.
.
.
HINT 2:
Question: Did the man die from his own doing?

Answer: Yes .
.
.
.
.
SOLUTION:
The man committed suicide with an icicle.

PROBLEM:
Frank leaves home.  When he tries to return, a man wearing a mask blocks his path.

1.) What is Frank doing?
2.) What is the masked man's occupation?
3.) Where is Frank's "safe place?".
.
.
.
.
HINT 1:
Question: Does this happen to Frank frequently?

Answer: Yes 
.
.
.
HINT 2:
Question: Does Frank enjoy the experience?

Answer: Yes.
.
.
.
.
SOLUTION:
1.) Playing Baseball
2.) A Catcher
3.) 3rd Base

PROBLEM:
A woman is seated and is writing.  There is a thunderstorm outside and she dies as a consequence.  How did she die?.
.
.
.
.
HINT 1:
Question: Was she writing at a desk or table?

Answer: No .
.
.
HINT 2:
Question: Was she doing her job when writing?

Answer: Yes.
.
.
.
.
SOLUTION:
She was a skywriter.  Lightning struck her airplane and she crashed

PROBLEM:
 Melissa and Jessica were working on the computer along with their friends Sandy and Nicole.  Suddenly, I heard a crash and then lots of shouts.  I rushed in to find out what was going on, finding the computer monitor on the ground, surrounded with broken glass!  Sandy and Jessica spoke almost at the same time:

Jessica saying, "It wasn't me!"
Sandy saying, "It was Nicole!"
Melissa yelled, "No, it was Sandy!"
With a pretty straight face Nicole said, "Sandy's a liar."

Only one of them was telling the truth, so who knocked over the monitor?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION:
Nicole was telling the truth; Jessica broke the monitor.

If only 1 of the 4 was telling the truth, that means that the other 3 were lying.  By using deductive reasoning, one would conclude that the only possibility with the presented facts is that Jessica was lying when she said, "It wasn't me," Sandy was lying when she said, "It was Nicole," and Melissa also lied when she said, "No, it was Sandy."  This leaves Nicole as the truth-teller, revealing Jessica as the culprit, having stated a direct lie when she said "It wasn't me!"

PROBLEM:
Mary had a coin purse with fifty coins, totaling exactly $1.00.  Unfortunately, while counting her change, she dropped one coin.  What is the probability that it was a penny?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION: 
There is an 85% probability that Mary dropped a penny.  There are two (and only two) combinations of 50 coins that will add up to $1.00.  These are:

40 Pennies, 2 Dimes, 8 Nickels, and
45 Pennies, 2 Dimes, 2 Nickels, 1 Quarter

With the first scenario alone, there would be a 80% probability, and the second scenario alone equates a 90% probability, respectfully.  But because we don't know which she had, the probability is the average of the two, or 85%

PROBLEM:
A rope burns non-uniformly for exactly one hour.  How do you measure 45 minutes, given two such ropes?.
.
.
.
.
.
.
.
.
.
SOLUTION:
Yes.  There are only 2 puzzles being spoken of: this one, and the one before this one.  The entire question could be rephrased like this:

If the puzzle you solved before this one was harder than this one, was the puzzle you solved before this one harder than this one?

Obviously, the answer to the question is simply yes